Das ist mein Blog.

Hier gibts, was ich tue, getan habe und vielleicht tun werde. Auch, wenn und weil das total unwichtig für den weiteren Verlauf der Geschichte ist. Viel Spaß damit.

Wer mich möglichst zeitnah erreichen und/oder beschimpfen will, versuche dies per Email (s.u.), per Twitter, auf Facebook oder im ircnet oder suche mich persönlich auf.

TMG §5 Kontaktdaten.

RSS-Feed Startseite

Einträge nach Kategorien

Einträge nach Datum

RSS-Feed
Startseite

07.01.2007

17:00 Uhr  Geolocating (web2.03)

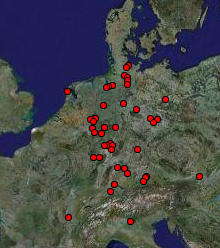
Eine weitere Möglichkeit, pseudointeraktive webzwonullige Vermaschungsmöglichkeiten zu schaffen. Grundlage für die nebenstehende Karte ist der Vlocate-Service, der wiederum auf den inzwischen zahlreich im Netz verfügbaren Datenbanken, die IP-Nummern bzw. Netzteile mit Ortsdaten wie z.B. GeoLite Country verknüpft.

Hier eine sehr, sehr primitive, aber dafür sehr anschauliche Version

Mit Hilfe von entsprechenden Datenbanken kann man dann rausfinden, wie die Nutzer z.B. einer Webseite über die Welt verteilt sind, und ob es sich lohnt, z.B. eine Sprachversion in koreanisch zu basteln.

Leider ist die von vlocate verwendete IP-Datenbank nur mäßig präzise - dafür ist der Service aber auch kostenlos; bzw gaukelt die Verbindung von Provider-Daten mit irre hochauflösenden Satellitendaten eine Genauigkeit vor, die die IP-Locations einfach nicht haben.

Wer sich auch in der Karte verewigen möchte, muß diesen Artikel direkt, also nicht per rss lesen und dabei javascript erlauben - rss/xml kann zum Glück kein javascript.

Irgendwas ist ja immer.

Ab hier wirds anstrengend.
Zonix: Du kannst nun aufhören, zu lesen. Alle anderen auch, die sich nicht für Navigation an sich und die Seemeile im besonderen interessieren.

Nun sollte ich noch erklären, warum 1,852km (auch genannt: 1 nautische Meile) so ein tolles Maß ist, um auf der Erde zu navigieren.
Es ereilte mich bereits eine ungeduldige und fragende Mail dazu. Nun gut.

Eine Seemeile ist eben der sechzigste Teil eines Breitengrades, also eine Bogenminute. Was ein Breitengrad genau ist, habe ich noch nicht erklärt. Im Gegensatz zu den Längengraden schneiden sich Breitenkreise nicht an irgendeinem Nullpunkt (so, wie die Längengrade an den Polen), sondern sind parallel zueinander ausgerichtet. Die Nullmarke für die Breitenkreise ist der Äquator, der genau in der Mitte zwischen Nord- und Südpol liegt, er steht senkrecht zur Drehachse der Erde, die zwischen den beiden Polen verläuft.
Das hat einen zwei große Vorteile:

Der Abstand zwischen zwei Breitengraden ist überall auf der Erde genau gleich, das ist bei den Längengraden nicht der Fall, weil sie sich alle im Pol treffen.

Die Breitengrade stehen immer genau rechtwinklig zu den Längengraden, da sie ja parallel zum Äquator liegen.

Um die Breite eines Ortes zu bestimmten, reichen sehr primitive Winkelmeßinstrumente aus - durch Beobachtung der Gestirne und der Messung des Winkels zwischen ihrer Position im Zenith und dem Horizont ließ sich bereits im Mittelalter die Breite eines Ortes verläßlich bestimmten - so breitelten sich auch die ersten Entdecker durch die Weltmeere und trafen erstaunlich genau Inseln, Städte (bei der Heimreise) usw wieder, wenn deren Breite (bzw. der Stand eines Gestirns von diesem Ort aus gemessen) bekannt war, ohne eine genau gehende Uhr haben zu müssen - diese ist allerdings für die Bestimmung der geografischen Länge eines Ortes extrem wichtig. Wenn das Thema interessiert, es gibt ein sehr schönes Buch dazu: Längengrad.
Es gibt 180 Breitenparallele, je 90 Richtung jeden Pols - der Pol selbst ist dann auf 90° nördlicher bzw südlicher Breite.

Die Seemeile funktioniert als Maß auch, wenn man die tatsächlichen Eckdaten einer Erde (oder des Jupiters) gerade nicht zur Hand hat - oder nur über sehr ungenaue Schätzungen verfügt, weil sie ein geometrisches Maß ist.

Die Erde hat einen Radius von etwa 6.370 km, daraus kann man leicht den Umfang berechnen (40.000 km). Teilt man diesen Umfang durch 360 Grad, und dann noch mal durch 60 (Minuten), erhält man eben genau diese ominösen 1.852 km, die einer Seemeile oder eben einer Bogenminute entsprechen.

Wenn man nun versucht, so etwas gewölbtes wie die Erde (ein sphärisches Objekt, ziemlich dreidimensional) auf Papier abzubilden (um z.B. eine Karte zu erzeugen), ergibt sich das Problem, daß Papier selbst erstmal ziemlich flach (zweidimensional) ist. Daraus ergeben sich ziemliche Verzerrungen, die für genaue Karten sehr problematisch sind. Das kann jeder ausprobieren, einfach mal eine Orange in ganz dünnes Papier einwickeln, die dabei entstehenden überflüssigen Ecken nach innen wegfalten, ein paar Punkte drauf malen oder drei Reißzwecken reindrücken, die Abstände der Reißzwecken mit Nähgarn o.ä. ausmessen und notieren (wer richtig wütig ist, versucht auch noch, die Winkel zwischen den Punkten zu bestimmen). Nun die Apfelsine auswickeln, Papier glattstreichen und den Abstand der Punkte noch mal messen.

Deswegen gibt es für Karten bestimmte Projektionsformen, die versuchen, die Kugelgestalt der Erde möglichst ohne oder aber mit bekannten, vernachlässigbaren Fehlern abzubilden. Sehr beliebt (außer für Polregionen) ist da die Mercator-Projektion, die die Erde in einen Papierzylinder aus Butterbrotpapier legt, der am Äquator anliegt. Dann wird im Erdmittelpunkt eine Lampe angemacht und die Erdoberfläche auf semitransparent geschaltet und abgezeichnet (Wer einen klassischen, von innen beleuteten Globus hat, kann das tatsächlich mal tun).

Wenn man diesen Zylinder nun ausrollt, bekommt man ein verzerrtes Abbild der Erde, Erdmassen in Äquatornähe werden im Verhältnis zu Regionen in Polnähe klein (also 1:1) abgebildet, je weiter der Abstand zwischen Globusoberfläche Zylinder wird, desto größer werden die Landmassen.
Eine richtige Mercatorkarte wird deswegen in N-S-Richtung angepaßt (gedehnt), so daß man an jedem Punkt richtungs- und winkeltreu ist, aber gleichzeitig mehrere Maßstäbe verwendet und nicht flächentreu ist.

Eine richtige Mercatorprojektion läßt sich also eigentlich nur rechnerisch, nicht zeichnerisch erzeugen.

Ich merke gerade, daß das hier deutlich zu weit führt. Wen das Thema genauer interessiert: Eine sehr fundierte Darstellung (die o.g. aus Wikipedia ist im Detail falsch) findet man unter: http://www.kowoma.de/gps/geo/Projektionen.htm, daher stammt auch die Grafik.

Wichtig ist: Eine Karte zur Navigation muß winkel- und streckentreu sein - sonst kann man nicht navigieren. Gleichzeitig ist es sehr hilfreich, wenn Längen- und Breiten rechtwinklig zueinander verlaufen, es gibt Kartenprojektionen, wo dies nicht der Fall ist.

Seekarten sind in gemäßigten Breiten eben Mercatorkarten, und sie haben an den Kartenrändern eine direkte Möglichkeit, Länge und Breite abzulesen. Da der Abstand zwischen zwei Breitengraden eben genau 60 Seemeilen sind, kann sehr schnell Distanzen aus der Karte nehmen (mit einem Marinezirkel) und an den linken oder rechten Rand halten, um die Entfernung zu erfahren. Dies geht eben auch bei Punkten, die nicht genau in N-S-Richtung liegen, sondern beliebig, da durch die Kartenprojektion Winkel- und Strecken-Treue für diesen Kartenausschnitt gewährleistet sind.
Mit der Einschränkung, daß dies nicht auf sehr kleinmaßstäblichen Karten (Überseglern) funktioniert, und daß man die Entfernung immer auf ungefähr der gleichen Breite am Kartenrand abmessen muß, auf der die beiden zu messenden Punkte auch liegen, da sich ja auch innerhalb der Karte der Maßstab immer leicht ändert (bei sehr großmaßstäblichen Karten ist das allerdings neben allen anderen möglichen Fehlern und Ungenauigkeiten zu Vernachlässigen - zum durch die Prüfung fallen reicht es aber trotzdem).

Desweiteren gibt es in Luft- und Seefahrt ein direkt von der Seemeile abhängendes Geschwindigskeitsmaß, den Knoten (also Seemeile pro Stunde). Damit kann man dann nicht nur Entfernungen sehr leicht aus einer Karte heraus messen, sondern auch gleich (Ankunfts-)Zeiten und Geschwindigkeiten, in dem man ein Vielfaches der aktuellen Geschwindigkeit (so sie einigermaßen gleichförmig ist) am Kartenrand in Seemeilen in den Zirkel nimmt, und dann die zu bewältigende Strecke abzirkelt.

Zu den Fragen in Hans ihm seiner Mail:
Wo ist dann der praktische Nutzen "zu Lande"?
Den gibts nur, wenn man wirklich 'navigiert', und nicht, wenn man nach Straßenatlas fährt. Ist man auf Straßen angewiesen, macht Navigation im klassischen Sinne keinen Sinn, auch nicht auf dem Wasser. Dort ist es dann einfacher, Tonnenpärchen zu zählen. Erst, wenn man eine Bewegungsrichtung relativ frei wählen kann (Hochsee, Wüste und in der Luft) oder wenn man es muß, z.B. beim Bau von neuen Straßen, Eisenbahntrassen usw. macht es Sinn, im Erdsinne richtig zu navigieren.

Da gibt es doch speziell projizierte Seekarten, das habe ich ganz schwach in Erinnerung. Die unterscheiden sich nochmal wie von der Land-Karte?
Siehe oben. Landkarten, insbesondere genauere Landkarten wie Meßtischblätter und Co sind transversale Zylinder-Projektionen, die also nicht den Äquator am Zylinder anliegen haben, sondern den Meridian, der in der Mitte des zu betrachtenden Kartenausschnittes liegt. Gängige transversale Kartenprojektionen sind z.B. Gauss-Krüger und das UTM-Gitter.

P.S. Auch der Meter ist ein Erdmaß - er ist der zehnmillionste Teil des Abstands zwischen Pol und Äquator - aber eben ein sehr unhandliches.

Und noch was: Die Karte mit den roten Punkten oben ist auch ne Mercatorkarte, wie die Karte in der Tagesschau. Immer gut zu erkennen an dem im Vergleich zu Afrika wirklich riesigen Grönland.

[Kategorie: /gis] - [permanenter Link] - [zur Startseite]